Jacobian matrix là gì? Ứng dụng của Jacobian matrix trong thực tế

Trong bối cảnh công nghệ AI và ngành robot học (robotics) đang bùng nổ, các mô hình hiện nay thường xử lý hàng trăm biến đầu vào và đầu ra phức tạp. Theo Stanford University, 78% các doanh nghiệp toàn cầu đã ứng dụng AI ít nhất vào một lĩnh vực, cho thấy hệ thống AI đang dần trở thành tiêu chuẩn trong hoạt động doanh nghiệp. Trong bối cảnh đó, Jacobian matrix trở thành công cụ toán học thiết yếu, giúp mô hình hiểu rõ mối quan hệ giữa sự thay đổi của đầu vào và đầu ra. Hãy cùng VNPT AI tìm hiểu về Jacobian matrix là gì trong bài viết dưới đây.

Jacobian matrix là gì?

Jacobian matrix là một cấu trúc toán học dùng để biểu diễn mối quan hệ giữa các biến đầu vào và nhiều biến đầu ra trong một hệ thống. Ma trận này cho thấy mức độ biến thiên của các biến đầu ra khi các biến đầu vào thay đổi.

Trong machine learning, Jacobian matrix đặc biệt hữu ích với các mô hình và phép biến đổi đa biến. Jacobian matrix làm rõ mối liên hệ giữa đầu vào và đầu ra, giúp phân tích ảnh hưởng của từng biến. Từ đó, việc tối ưu mô hình, huấn luyện mạng nơ-ron và đảm bảo ổn định cho thuật toán học máy được cải thiện đáng kể.

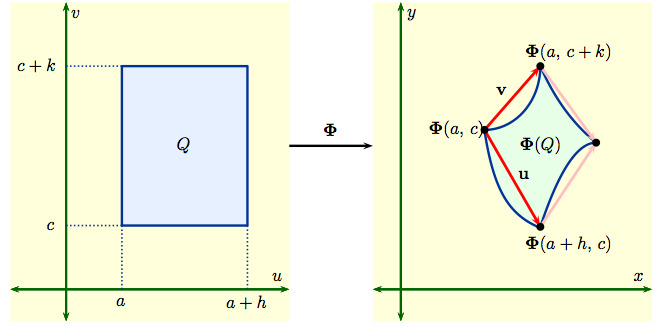
Vai trò của ma trận Jacobian

Ma trận Jacobian đóng vai trò quan trọng trong nhiều lĩnh vực tính toán và khoa học dữ liệu, cụ thể như:

• Phân tích sự biến đổi của hệ thống: Ma trận Jacobian cho phép đánh giá mức độ thay đổi của đầu ra khi các biến đầu vào thay đổi, giúp nhận diện các chiều ảnh hưởng mạnh hoặc yếu trong một mô hình.
• Hỗ trợ tối ưu hóa mô hình: Trong quá trình huấn luyện mạng nơ-ron, Jacobian matrix giúp theo dõi sự lan truyền gradient, từ đó hạn chế hiện tượng mất hoặc nổ gradient và cải thiện khả năng hội tụ của thuật toán.
• Đánh giá độ ổn định của thuật toán: Thông qua việc phân tích giá trị riêng của ma trận Jacobian, các nhà nghiên cứu có thể xác định mức độ ổn định của hệ thống, đặc biệt quan trọng trong các mô hình động hoặc học tăng cường.
• Ứng dụng trong chuyển đổi tọa độ và mô phỏng: Trong toán học và đồ họa máy tính, ma trận Jacobian được sử dụng để biến đổi không gian, ví dụ khi ánh xạ từ một hệ tọa độ sang hệ khác hoặc mô phỏng sự thay đổi hình dạng.

Ứng dụng của Jacobian Matrix

Ma trận Jacobian được áp dụng rộng rãi trong nhiều lĩnh vực khoa học và công nghệ hiện đại, điển hình như:

Ma trận Jacobian trong học máy và học sâu

Trong học máy, đặc biệt khi làm việc với mạng nơ-ron sâu, ma trận Jacobian đóng vai trò hỗ trợ việc lan truyền thông tin ngược về các lớp trước đó (backpropagation). Mỗi lớp mạng có thể được hình dung như một phép biến đổi từ dữ liệu đầu vào thành đầu ra, và ma trận Jacobian ở mỗi lớp cho biết mức độ thay đổi của gradient khi đi qua phép biến đổi đó.

Quá trình truyền ngược được thực hiện theo chuỗi:

∂L∂x =  ∂L∂y.Jf(x)

Ở đây, L là hàm tính lỗi, y=f(x) là đầu ra của lớp, và Jf(x) biểu thị ma trận Jacobian. 

Khi hiểu rõ và tối ưu ma trận Jacobian, việc huấn luyện mạng nơ-ron sẽ trở nên ổn định hơn và tốc độ hội tụ cũng được cải thiện.

Ngoài ra, Jacobian matrix còn hữu ích trong các tác vụ như:

• Khả năng diễn giải mô hình (Interpretability): Phân tích Jacobian matrix cho phép nhận diện đầu vào nào ảnh hưởng nhiều nhất đến đầu ra, từ đó tăng khả năng diễn giải quyết định của mô hình và hỗ trợ việc xây dựng các hệ thống AI minh bạch hơn.
• Học chuyển giao (Transfer Learning): Khi áp dụng mô hình đã huấn luyện cho một bài toán mới, Jacobian matrix cung cấp thông tin về mức độ thích ứng giữa dữ liệu cũ và dữ liệu mới. Điều này giúp xác định những phần nào của mạng cần tinh chỉnh và  tiết kiệm thời gian huấn luyện lại.

Ma trận Jacobi trong robot

Ma trận Jacobian còn giúp điều khiển và tối ưu hoạt động của robot, đặc biệt khi cần đảm bảo chuyển động chính xác, ổn định và an toàn. 

• Xác định chuyển động của tay máy: Jacobian cho phép chuyển đổi sự dịch chuyển ở các khớp thành chuyển động cụ thể của đầu gắp hoặc công cụ. Nhờ vậy, robot có thể thực hiện các thao tác như hàn, sơn hay lắp ráp một cách chính xác.
• Phát hiện và tránh điểm giới hạn chuyển động: Một số vị trí khiến robot khó di chuyển linh hoạt, được gọi là điểm kỳ dị (singularities). Jacobian hỗ trợ phát hiện các vị trí này để điều chỉnh thiết kế hoặc quỹ đạo giúp robot vận hành mượt mà.
• Điều chỉnh lực tác động: Thông tin từ ma trận Jacobian giúp phân bổ lực hợp lý qua các khớp, tránh gây hỏng hóc hoặc làm biến dạng đồ vật.

>>> Bạn có thể quan tâm: Transfer learning là gì?

Tạm kết

Hy vọng bài viết trên của VNPT AI cung cấp thông tin hữu ích cho bạn đọc về Jacobian matrix. Ma trận này giúp dự đoán chuyển động của các bộ phận dựa trên sự dịch chuyển của khớp, đồng thời hỗ trợ phát hiện những điểm có thể gây hạn chế chuyển động để kịp thời điều chỉnh. Không chỉ vậy, Jacobian matrix còn giúp kiểm soát lực tác động của robot, đảm bảo an toàn khi thao tác với các vật dễ vỡ hoặc yêu cầu độ chính xác cao. Nhờ những ứng dụng đó, Jacobian matrix đã trở thành nền tảng quan trọng trong sản xuất công nghiệp, phẫu thuật robot và nhiều hệ thống tự động hóa khác. Việc nghiên cứu và tối ưu ma trận này sẽ mở ra cơ hội cải thiện hiệu suất và tăng tính linh hoạt cho robot trong tương lai.