KL divergence là gì? Ứng dụng trong thực tế và rủi ro khi triển khai

Trong quá trình xây dựng mô hình AI, việc đánh giá độ "khớp" của mô hình với dữ liệu thực luôn là thách thức lớn. KL Divergence chính là một giải pháp hữu ích để giải quyết vấn đề này. Công cụ này cho biết lượng thông tin bị mất mát khi phân phối dự đoán xấp xỉ phân phối thực, cung cấp điểm số lỗi để mô hình biết và tự điều chỉnh sao cho chuẩn xác hơn. Trong bài viết dưới đây, hãy cùng VNPT AI đi tìm hiểu sâu hơn về khái niệm, tính ứng dụng cùng những rủi ro khi áp dụng của KL Divergence.

KL divergence là gì?

KL Divergence (độ phân kỳ Kullback–Leibler Divergence - KL) là một khái niệm quan trọng trong lý thuyết thông tin. Đây là thước đo thống kê, thường dùng để định lượng sự khác biệt giữa hai phân phối xác suất: phân phối thực tế và phân phối tham chiếu.

Về bản chất, phân kỳ Kullback–Leibler cho biết lượng thông tin bị mất mát khi ta sử dụng phân phối Q để xấp xỉ phân phối P. Do đó, KL thường được diễn giải gần giống như một "khoảng cách", nhưng không phải là khoảng cách đối xứng theo nghĩa toán học giữa hai phân phối.

Nền tảng toán học của phân kỳ Kullback–Leibler

Độ phân kỳ KL được định nghĩa là số bit cần thiết để chuyển đổi một phân phối này sang dạng một phân phối khác. Về mặt toán học, KL Divergence được định nghĩa dưới dạng công thức như sau:

KL(P‖Q)=x ∊ XP(x) * log (P(x)Q(x))

Trong đó:

• P(x) là phân phối xác suất thực tế
• Q(x) là phân phối tham chiếu hoặc phân phối mô hình
• P(x)/Q(x) phản ánh mức độ khả dĩ của biến cố x theo phân phối P so với phân phối Q

Một điểm đáng chú ý là KL Divergence có mối quan hệ chặt chẽ với Cross-Entropy (mất mát logarit) trong học sâu. Cả hai đều là công cụ định lượng sự khác biệt giữa các phân phối xác suất, do đó thường được dùng thay thế hoặc kết hợp trong các bài toán tối ưu mô hình.

Nếu ta mở rộng công thức trên, ta thấy KL Divergence chính là hiệu số giữa Cross-Entropy và Entropy. Công thức có thể được viết lại như sau:

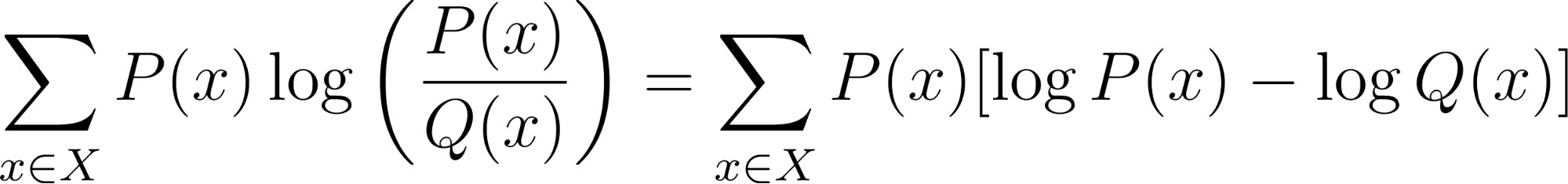
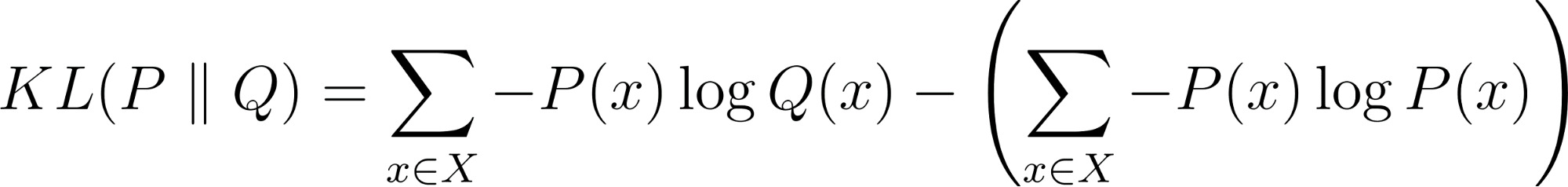
Cross-Entropy (Thành phần bên trái):

Entropy (Thành phần bên phải):

KL Divergence chính là sự chênh lệch giữa hai chi phí đó:

Ứng dụng của KL divergence

KL divergence được ứng dụng nhiều trong các lĩnh vực thực tiễn như học máy và khoa học dữ liệu. Cụ thể, mô hình này đảm nhận một số công việc sau:

• Đánh giá mô hình: KL Divergence đo khoảng cách giữa phân phối dự đoán và phân phối nhãn thực tế, từ đó phản ánh mức độ chính xác của mô hình.
• Phát hiện sự dịch chuyển dữ liệu: KL Divergence giúp theo dõi sự biến động của dữ liệu theo thời gian, cung cấp thông tin chi tiết về bản chất của biến đổi và đưa ra cảnh báo về nhu cầu huấn luyện lại mô hình.
• Hàm mất mát trong mạng nơ-ron: Trong các bài toán phân loại, KL Divergence được sử dụng như một hàm mất mát. Bằng cách tối thiểu hóa KL Divergence, mô hình được tối ưu hóa và phân phối dự đoán tiến gần nhất tới phân phối nhãn thực.
• Biến thể suy luận: Trong các mô hình như Variational Autoencoders (VAEs), KL Divergence giữ vai trò điều chỉnh phân phối tiềm ẩn, đảm bảo nó gần đúng với phân phối chuẩn đã biết, hỗ trợ việc tạo mẫu hiệu quả hơn.
• Mô hình tạo sinh (Generative Models): Trong GANs (Generative Adversarial Networks), KL Divergence giúp so sánh phân phối dữ liệu thật và dữ liệu giả, hỗ trợ quá trình cạnh tranh giữa bộ tạo (generator) và bộ phân biệt (discriminator).
• Học tăng cường: Các thuật toán tối ưu như Trust Region Policy Optimization (TRPO) áp dụng ràng buộc KL Divergence để kiểm soát việc cập nhật chính sách. Điều này nhằm đảm bảo rằng các bước cập nhật không quá lớn, từ đó duy trì sự ổn định trong huấn luyện và tránh các thay đổi đột ngột làm hỏng mô hình.

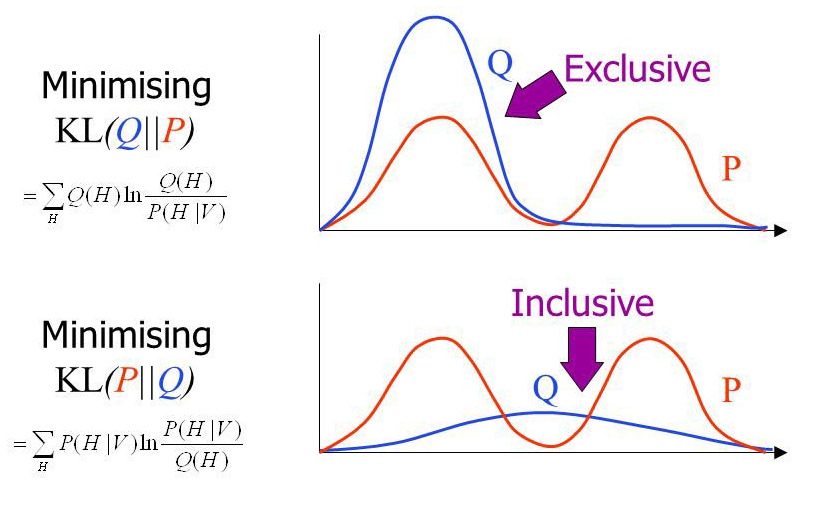
Hạn chế và rủi ro của Kullback–Leibler (KL) divergence

Mặc dù là một công cụ mạnh mẽ trong lĩnh vực Machine Learning (Học máy) và Trí tuệ nhân tạo AI, KL Divergence vẫn tồn tại nhiều hạn chế và rủi ro cần được cân nhắc khi áp dụng:

• Tính bất đối xứng: KL(P‖Q) không bằng KL(Q‖P), do đó nó không phải là thước đo khoảng cách đối xứng. Điều này có thể gây hiểu nhầm khi so sánh hai phân phối.
• Vấn đề phân phối không khớp: Nếu Q(x) = 0 trong khi P(x) > 0, giá trị log(P/Q) sẽ tiến tới vô cực. Trường hợp này khiến KL Divergence không ổn định và khó sử dụng trong thực tế.
• Ảnh hưởng của dữ liệu thưa: Với các đặc trưng phân loại có số lượng giá trị quá lớn (high-cardinality categorical features), KL Divergence dễ bị nhiễu, dẫn đến ước lượng sai lệch.
• Độ tin cậy hạn chế khi khác tham số: Khi hai phân phối có tham số trung bình hoặc phương sai khác biệt quá lớn, KL Divergence không cung cấp kết quả đáng tin cậy.
• Đơn vị đo không nhất quán: KL Divergence có thể được tính bằng “nats” hoặc “bits”. Nếu không ghi rõ cơ số log được sử dụng, kết quả có thể gây nhầm lẫn trong diễn giải.

Tạm kết:

Tóm lại, KL Divergence là công cụ toán học quan trọng trong lý thuyết thông tin và học máy có khả năng định lượng thông tin bị mất mát khi mô hình xấp xỉ dữ liệu thực. Đồng thời, KL Divergence đóng vai trò then chốt trong việc huấn luyện VAEs và các mô hình học sâu khác. Tuy nhiên, việc triển khai đòi hỏi sự cẩn trọng về tính bất đối xứng và đặc biệt cần lưu ý khi phân phối dự đoán không bao phủ được phân phối thực tế.