Principal component analysis (PCA) là gì? Cách thức hoạt động

Theo báo cáo "Why Big Data Projects Fail? A Systematic Literature Review", một trong những nguyên nhân chính khiến các dự án big data (dữ liệu lớn)  thất bại là do gặp thách thức kỹ thuật, đặc biệt là về chất lượng và tích hợp dữ liệu. Vì vậy, nhiều đơn vị đã tìm đến Principal Component Analysis (PCA) - phương pháp giúp giảm mạnh số chiều dữ liệu. Vậy PCA là gì và hoạt động như thế nào? Hãy cùng VNPT AI khám phá trong bài viết dưới đây!

Principal component analysis (PCA) là gì?

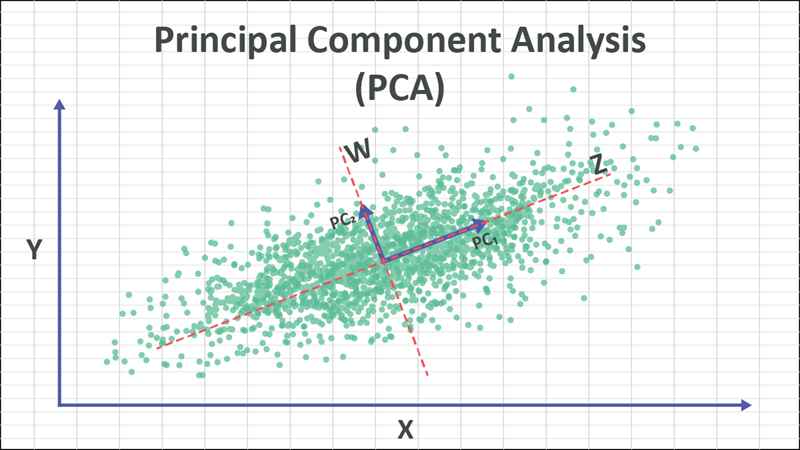
Principal component analysis (PCA) là một kỹ thuật thống kê dùng để giảm chiều dữ liệu (dimensionality reduction). Phương pháp này biến đổi dữ liệu có nhiều biến đầu vào thành một tập nhỏ hơn gọi là các thành phần chính (principal components), nhưng vẫn giữ lại phần lớn thông tin quan trọng. 

Ngoài ra, PCA còn giúp phát hiện xu hướng, mẫu dữ liệu và loại bỏ các vấn đề như đa cộng tuyến (multicollinearity) hay quá khớp (overfitting). Đồng thời, kỹ thuật này cũng có khả năng đơn giản hóa dữ liệu để dễ dàng trực quan hóa và xử lý bằng các thuật toán học máy (machine learning). Nhờ những ưu điểm này, PCA được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như: phân tích dữ liệu, xử lý ảnh, nhận dạng mẫu,.…

Principal component analysis (PCA) hoạt động như thế nào?

Quá trình hoạt động của PCA bao gồm các bước cơ bản sau:

• Bước 1: Chuẩn hóa dữ liệu: Dữ liệu được chuẩn hóa về cùng một thang đo bằng cách trừ đi giá trị trung bình và chia cho độ lệch chuẩn.
• Bước 2: Tính ma trận hiệp phương sai: Bước này nhằm tính toán ma trận hiệp phương sai để xác định mối quan hệ và mức độ tương quan giữa các biến, nhận diện thông tin dư thừa
• Bước 3: Phân rã trị riêng và vector riêng: Từ ma trận hiệp phương sai, PCA tìm ra các eigenvectors (vector riêng) và eigenvalues (trị riêng). Các vector riêng xác định các hướng có độ biến thiên dữ liệu lớn nhất, còn các trị riêng cho biết lượng thông tin mà mỗi hướng mang lại.
• Bước 4: Chọn thành phần chính: Các eigenvectors được sắp xếp theo thứ tự giảm dần của eigenvalues. Những vector có trị riêng cao nhất sẽ được chọn làm thành phần chính vì chúng chứa nhiều thông tin nhất.
• Bước 5: Chiếu dữ liệu lên không gian mới: Dữ liệu gốc được chiếu lên các thành phần chính đã chọn. Kết quả thu được là một tập dữ liệu có số chiều thấp hơn nhưng vẫn giữ được hầu hết các đặc trưng quan trọng, giúp trực quan hóa dễ dàng hơn và tăng hiệu quả cho các thuật toán học máy.

Các biến thể mở rộng của PCA

Mặc dù PCA là một phương pháp giảm chiều dữ liệu tuyến tính mạnh mẽ, nhưng vẫn tồn tại những hạn chế nhất định. Chính vì vậy, nhiều biến thể và mở rộng của PCA đã ra đời nhằm khắc phục những nhược điểm này.

Kernel PCA (KPCA)

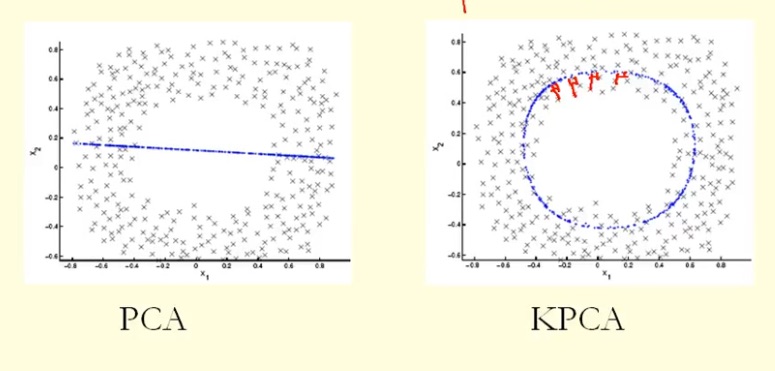
Kernel PCA mở rộng PCA truyền thống bằng cách sử dụng kernel trick để ánh xạ dữ liệu từ không gian gốc sang một không gian đặc trưng có chiều cao hơn. Nhờ phép biến đổi này, các mối quan hệ phi tuyến trong dữ liệu gốc có thể được biểu diễn dưới dạng tuyến tính trong không gian mới, giúp phát hiện các cấu trúc phức tạp mà PCA truyền thống bỏ qua. Biến thể KPCA được ứng dụng nhiều trong các lĩnh vực như: nhận diện khuôn mặt, phân cụm dữ liệu phi tuyến và xử lý hình ảnh.

Sparse PCA (SPCA)

Sparse PCA bổ sung ràng buộc thưa (sparsity) vào các thành phần chính, nhờ đó mỗi thành phần chỉ liên quan đến một số biến nhất định. Nhờ vậy, kết quả  dễ diễn giải hơn và giảm nguy cơ quá khớp khi xử lý dữ liệu có số chiều rất lớn, chẳng hạn như phân tích văn bản hoặc dữ liệu gen.

Robust PCA (RPCA)

Robust PCA (RPCA) là một biến thể của PCA, được thiết kế để xử lý dữ liệu nhiễu hoặc có ngoại lai (outliers). Phương pháp này phân tách dữ liệu thành hai phần: (i) ma trận hạng thấp, biểu diễn cấu trúc chính, và (ii) ma trận thưa, chứa các giá trị bất thường. RPCA đặc biệt hữu ích trong các bài toán như: phát hiện gian lận tài chính, loại bỏ nền trong video giám sát, và phân tích các tập dữ liệu có sai số lớn.

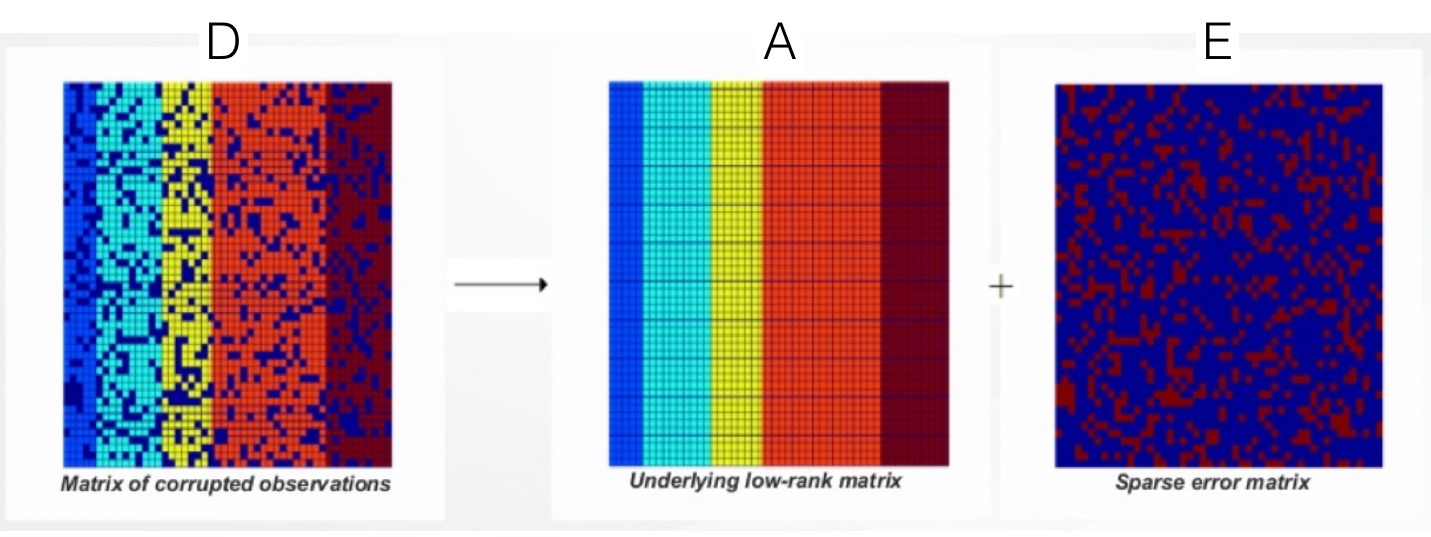
Incremental PCA (IPCA)

Incremental PCA giải quyết hạn chế về bộ nhớ của PCA truyền thống bằng cách tính toán dần dần trên từng lô dữ liệu nhỏ thay vì toàn bộ tập dữ liệu cùng lúc. Phương pháp này phù hợp cho các hệ thống xử lý dữ liệu lớn (Big Data) hoặc dữ liệu phát sinh liên tục (streaming data), chẳng hạn như phân tích log hệ thống hay giám sát dữ liệu thời gian thực.

Probabilistic PCA (PPCA)

Probabilistic PCA là phiên bản mở rộng của PCA truyền thống, được xây dựng trong khuôn khổ mô hình xác suất. khuôn khổ mô hình xác suất. Phương pháp này giả định rằng dữ liệu được sinh ra từ các biến tiềm ẩn và chịu ảnh hưởng của nhiễu Gaussian. Cách tiếp cận này giúp xử lý hiệu quả dữ liệu thiếu, đồng thời ước lượng được mức độ không chắc chắn của mô hình, mang lại nền tảng lý thuyết vững chắc hơn cho thống kê và học máy.

Ưu nhược điểm của Principal component analysis (PCA)

Một số ưu điểm nổi bật của PCA có thể kể đến như:

Ưu điểm

• Giảm chiều dữ liệu hiệu quả: PCA biến đổi tập dữ liệu ban đầu thành các thành phần chính chứa nhiều thông tin nhất, từ đó giúp việc xử lý và trực quan hóa dữ liệu trở nên đơn giản hơn.
• Loại bỏ nhiễu: PCA thường loại bỏ các thành phần có phương sai thấp, vì chúng chứa ít giá trị thực tiễn và có thể coi là nhiễu.
• Tăng tốc độ tính toán: Khi số lượng biến giảm, các thuật toán học máy hoạt động nhanh hơn và hiệu quả hơn. Đồng thời, PCA cũng giúp giải quyết vấn đề đa cộng tuyến khi các biến gốc có mối tương quan cao.
• Hỗ trợ trực quan hóa dữ liệu: PCA cho phép biểu diễn dữ liệu trong không gian hai hoặc ba chiều, giúp người dùng dễ dàng quan sát cấu trúc và phân bố của dữ liệu.

Nhược điểm

Bên cạnh những ưu điểm trên, PCA cũng tồn tại một số hạn chế:

• Giả định tính tuyến tính: PCA chỉ phù hợp với dữ liệu có cấu trúc tuyến tính. Khi dữ liệu có mối quan hệ phi tuyến phức tạp, PCA có thể không mang lại kết quả chính xác.
• Nhạy cảm với nhiễu và outliers: Các điểm bất thường dễ làm sai lệch phương sai, từ đó ảnh hưởng đến hướng của các thành phần chính.
• Khó giải thích kết quả: Các thành phần chính chỉ là sự kết hợp tuyến tính của nhiều biến ban đầu, vì vậy việc gán ý nghĩa cụ thể cho từng thành phần thường gặp khó khăn.
• Phụ thuộc vào việc chuẩn hóa dữ liệu: Nếu không chuẩn hóa, các biến có thang đo lớn sẽ chi phối kết quả, gây sai lệch trong phân tích.
• Đòi hỏi tài nguyên lớn với dữ liệu khổng lồ: Khi áp dụng cho tập dữ liệu rất lớn, PCA có thể tiêu tốn nhiều thời gian tính toán và bộ nhớ.

Ứng dụng của Principal component analysis

Một số ứng dụng tiêu biểu của PCA bao gồm:

• Trực quan hóa dữ liệu: PCA cho phép chiếu dữ liệu có số chiều cao xuống không gian 2D hoặc 3D. Nhờ đó giúp người phân tích dễ dàng quan sát xu hướng, phát hiện cụm dữ liệu hoặc điểm ngoại lệ. Đây là bước quan trọng trong việc khám phá dữ liệu và trình bày kết quả một cách trực quan.
• Tiền xử lý cho Machine Learning: PCA thường được dùng để giảm chiều dữ liệu trước khi huấn luyện mô hình, giúp rút ngắn thời gian xử lý và giảm nguy cơ quá khớp (overfitting). Đồng thời, việc giữ lại các đặc trưng quan trọng nhất cũng giúp mô hình tổng quát hóa tốt hơn với dữ liệu mới.
• Trích xuất đặc trưng (Feature Extraction): PCA biến đổi các biến đầu vào có tương quan cao thành một tập nhỏ hơn gồm các thành phần không tương quan, giúp tăng khả năng giải thích và cải thiện hiệu suất mô hình, đặc biệt trong các bài toán phức tạp như xử lý văn bản hoặc phân tích bộ dữ liệu lớn.
• Nén dữ liệu và hình ảnh: PCA biểu diễn dữ liệu bằng ít thành phần hơn nhưng vẫn giữ lại phần lớn thông tin cần thiết, nhờ đó giảm dung lượng lưu trữ và tăng tốc độ truyền tải dữ liệu.
• Lọc nhiễu (Noise Filtering): PCA loại bỏ nhiễu và thông tin dư thừa bằng cách giữ lại các thành phần chính có phương sai cao nhất. Ứng dụng này đặc biệt hữu ích trong xử lý ảnh, âm thanh và tín hiệu, khi cần tập trung vào các đặc điểm cốt lõi.

Tạm kết

Hy vọng những thông tin hữu ích được VNPT AI chia sẻ trên đây đã giúp bạn đọc hiểu rõ hơn về khái niệm PCA là gì và cách thức hoạt động của kỹ thuật này. Là một phương pháp xử lý dữ liệu ưu việt, PCA đóng vai trò quan trọng trong việc đơn giản hóa dữ liệu và tăng tốc độ thuật toán. Tuy nhiên, để triển khai hiệu quả, doanh nghiệp cần chuẩn hóa dữ liệu đầu vào, thận trọng với dữ liệu nhiễu. Ngoài ra, đơn vị triển khai cũng nên cân nhắc áp dụng các biến thể khác của PCA trong bối cảnh cụ thể để khắc phục những hạn chế tồn tại. Việc áp dụng PCA đúng cách sẽ giúp doanh nghiệp tận dụng hiệu quả nguồn dữ liệu lớn, đồng thời hỗ trợ quá trình ra quyết định nhanh chóng và chính xác hơn.