Chain Rule trong AI: Chìa khóa tối ưu hóa mô hình học sâu hiện đại

Trong thời đại trí tuệ nhân tạo phát triển mạnh mẽ, những tiến bộ trong học máy (machine learning) đã làm thay đổi cách con người giải quyết vấn đề. Ẩn sau khả năng tự học của các mô hình AI là nền tảng toán học vững chắc, trong đó Chain Rule đóng vai trò then chốt giúp máy tính hiểu và tối ưu hóa quá trình học tập. Vậy Chain Rule là gì? Vai trò Chain Rule trong học máy ra sao? Hãy cùng VNPT AI tìm hiểu trong bài viết dưới đây.

Chain Rule là gì?

Chain Rule, hay quy tắc chuỗi, là phương pháp dùng để tính đạo hàm của hàm hợp, tức một hàm được hình thành bằng cách lồng ghép nhiều hàm đơn giản lại với nhau. Ý tưởng chính của quy tắc này là xem xét sự thay đổi của biến đầu vào lan truyền qua từng lớp của hàm.

Cụ thể:

• Giả sử có hàm g(x) nhận đầu vào là x.
• Kết quả của g(x) được coi như một biến trung gian u=g(x).
• Hàm f(u) lại nhận u làm đầu vào và cho ra kết quả.

Khi đó, hàm hợp được viết là: h(x)=f(g(x))

Quy tắc chuỗi chỉ ra rằng để tính đạo hàm của h(x), ta cần nhân hai bước biến thiên:

• Sự thay đổi của g(x) theo x, tức g′(x).
• Sự thay đổi của f(u) theo u, tức f′(u).

Công thức quy tắc chuỗi: h′(x)=f′(g(x))⋅g′(x)

>>> Đọc thêm: Jacobian matrix là gì?

Vai trò của quy tắc chuỗi trong công nghệ và AI

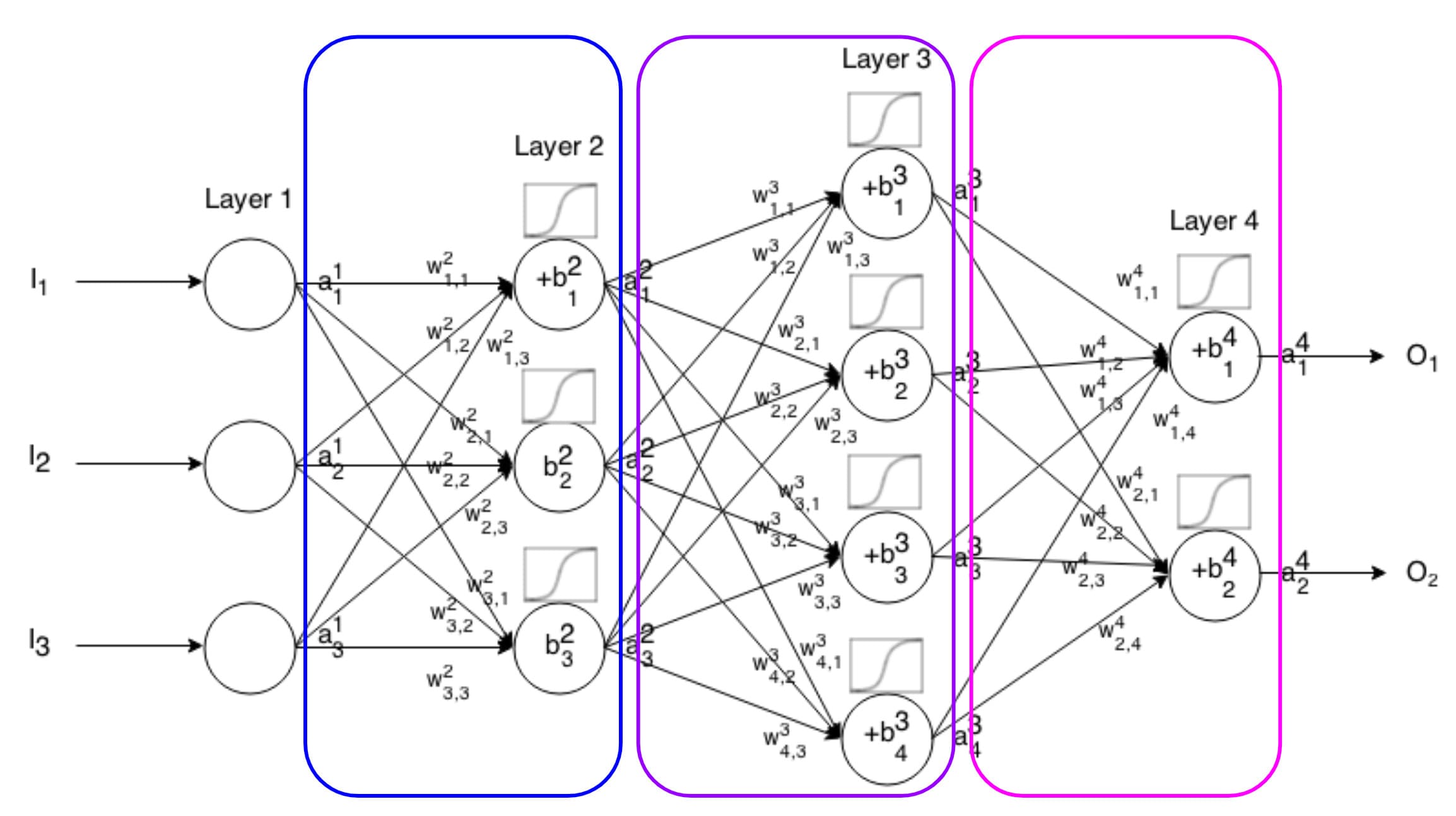
Quy tắc chuỗi giữ vai trò quan trọng trong quá trình backpropagation - nền tảng của huấn luyện mạng nơ-ron hiện đại. Nhờ quy tắc này, các mô hình học máy có thể điều chỉnh trọng số dựa trên tín hiệu sai số, từ đó học được mối quan hệ giữa đầu vào và đầu ra.

Cụ thể, trong học sâu, quy tắc chuỗi cho phép tính toán gradient một cách có hệ thống qua nhiều lớp của mạng, cho phép tính toán gradient một cách có hệ thống qua nhiều lớp của mạng. Từ đó giúp quá trình tối ưu hóa khả thi và hiệu quả, đặc biệt trong các kiến trúc phức tạp. Quá trình backpropagation sử dụng quy tắc chuỗi gồm các bước:

• Tính đầu ra (Forward Pass): Cho dữ liệu đi qua mạng để ra dự đoán.
• Tính sai số (Loss Calculation): So sánh dự đoán với kết quả thật.
• Tính gradient (Gradient Calculation): Dùng quy tắc chuỗi để tìm mức thay đổi cần thiết ở từng lớp.
• Cập nhật trọng số (Weight Updates): Điều chỉnh trọng số bằng các thuật toán để mô hình dự đoán chính xác hơn.

Ứng dụng của Chain Rule

Chain Rule được ứng dụng rộng rãi trong nhiều lĩnh vực, đặc biệt khi tính toán sự thay đổi của các hệ thống phức tạp qua nhiều giai đoạn biến đổi. Dưới đây là một số ứng dụng phổ biến:

• Backpropagation (Lan truyền ngược): Trong mạng nơ-ron, quy tắc chuỗi là chìa khóa giúp tính toán gradient (độ dốc) của hàm mất mát so với các trọng số. Nhờ đó, sai số được lan truyền ngược qua từng lớp, giúp mô hình biết cách điều chỉnh trọng số để học tốt hơn.
• Thuật toán tối ưu (Gradient Descent): Khi huấn luyện mô hình, quy tắc chuỗi hỗ trợ tính gradient của hàm mất mát theo từng tham số. Dựa vào gradient này, thuật toán tối ưu sẽ cập nhật tham số theo hướng làm giảm sai số nhanh nhất.
• Mạng nơ-ron hồi tiếp (RNNs): Trong các mô hình xử lý chuỗi dữ liệu như văn bản, giọng nói, quy tắc chuỗi giúp lan truyền gradient qua từng thời điểm, cho phép mạng học từ mối liên kết giữa các phần tử trong chuỗi.
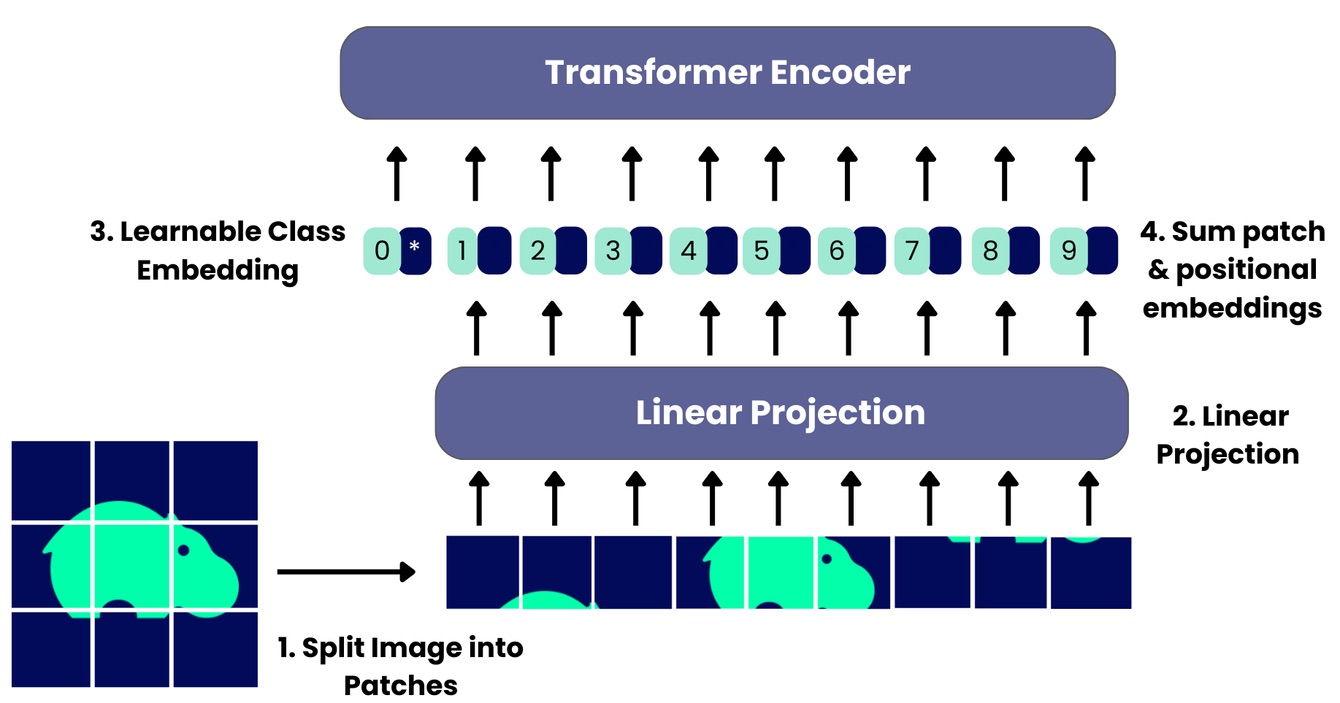
• Mạng nơ-ron tích chập (CNNs): Với các bài toán xử lý ảnh, quy tắc chuỗi giúp tính toán gradient trong các lớp tích chập, từ đó mạng học được cách phát hiện và sắp xếp các đặc trưng không gian (spatial features) một cách chính xác.

Thách thức và hạn chế của Chain Rule trong AI

Mặc dù quy tắc chuỗi là nền tảng quan trọng giúp các mô hình AI học hỏi và tối ưu, quá trình áp dụng trên các hệ thống phức tạp vẫn tồn tại thách thức và hạn chế:

• Vanishing Gradients trong các mạng nhiều tầng: Khi huấn luyện mạng nơ-ron có hàng nghìn lớp, một vấn đề phổ biến là gradient trở nên quá nhỏ khi lan truyền ngược qua nhiều tầng. Điều này làm cho các lớp ở đầu mạng khó học được đặc trưng quan trọng, khiến quá trình huấn luyện chậm và kém hiệu quả.
• Khả năng mở rộng với mô hình hàng tỷ tham số: Những mô hình AI khổng lồ với hàng tỷ tham số đặt ra thách thức lớn về tính toán và bộ nhớ. Việc cập nhật gradient cho toàn bộ tham số đòi hỏi hạ tầng xử lý song song mạnh mẽ và các kỹ thuật tối ưu tiên tiến.
• Chi phí tính toán cao: Mỗi lần áp dụng quy tắc chuỗi để tính đạo hàm qua nhiều lớp đòi hỏi lượng tính toán lớn, đặc biệt với mô hình có nhiều tham số.
• Ảnh hưởng của sai số tích lũy: Vì gradient được tính toán từng bước qua nhiều lớp, sai số làm tròn (rounding error) có thể tích lũy và ảnh hưởng đến độ chính xác, nhất là trong mô hình cực lớn.

Tương lai và xu hướng của quy tắc chuỗi trong AI

Khi trí tuệ nhân tạo phát triển, quy tắc chuỗi không chỉ được dùng trong các mô hình học máy truyền thống mà còn đóng vai trò trong những công nghệ tiên tiến:

Trong học máy lượng tử (Quantum Machine Learning - QML)

QML kết hợp kỹ thuật tối ưu cổ điển với sức mạnh tính toán lượng tử. Thay vì sử dụng backpropagation truyền thống, QML thường áp dụng parameter-shift rule, một dạng mở rộng của Chain Rule, để tính gradient cho các mạch lượng tử có tham số. Điều này giúp tối ưu các thuật toán lượng tử nhằm khai thác đặc tính độc đáo của trạng thái lượng tử.

Trong hệ thống tự hành

Xe tự lái và robot thông minh sử dụng học máy dựa trên gradient để phân tích dữ liệu cảm biến thời gian thực và cải thiện khả năng ra quyết định. Quy tắc chuỗi giúp các hệ thống này nhanh chóng điều chỉnh mô hình khi môi trường thay đổi liên tục.

Tạm kết

Hy vọng bài viết trên của VNPT AI đã giúp bạn đọc giải đáp những thắc mắc về Chain Rule. Đây không chỉ là công cụ toán học cơ bản mà còn là nền tảng cho sự phát triển của trí tuệ nhân tạo hiện đại. Nhờ Chain Rule, các mô hình học sâu có thể học hiệu quả hơn, tối ưu hóa hàng tỷ tham số và mở ra nhiều ứng dụng thực tiễn từ xe tự hành đến học máy lượng tử. Trong tương lai, Chain Rule sẽ tiếp tục được cải tiến để đáp ứng nhu cầu của các hệ thống AI ngày càng phức tạp và quy mô lớn.