Giải mã Eigenvalues và Eigenvectors: Khái niệm, cách tính và ứng dụng

Trong lĩnh vực phân tích dữ liệu và học máy, việc đơn giản hóa và tìm ra xu hướng cốt lõi của dữ liệu được đánh giá là rất quan trọng. Eigenvalues và Eigenvectors chính là bộ đôi hoàn hảo cho nhiệm vụ này. Eigenvalues Eigenvector được sử dụng để giảm chiều dữ liệu (Principal Component Analysis - PCA), phân tích trạng thái ổn định và tìm ra sự liên kết giữa các nguồn dữ liệu, từ đó có hướng khai thác hợp lý. Vậy, Eigenvalues Eigenvectors là gì, được tính toán như thế nào và ứng dụng ra sao trong thực tế?  Bài viết này của VNPT AI sẽ cung cấp cho bạn những thông tin hữu ích.

Eigenvalues và Eigenvectors là gì?

Eigenvalues và Eigenvectors (giá trị riêng và vector riêng) là hai công cụ quan trọng trong đại số tuyến tính, thể hiện cách một ma trận tác động lên không gian vector thông qua biến đổi tuyến tính. Các khái niệm này không chỉ giúp mô tả cách ma trận tác động lên không gian mà còn đóng vai trò nền tảng trong nhiều thuật toán quan trọng như giảm chiều dữ liệu (Principal Component Analysis - PCA).

Để dễ hình dung hơn, hãy tưởng tượng một phép biến đổi tuyến tính như một sự co giãn, xoay hoặc nén một không gian. Trong quá trình đó, hầu hết các vector sẽ bị thay đổi cả về hướng lẫn độ dài. Tuy nhiên, có những vector đặc biệt không bị thay đổi hướng, mà chỉ bị co giãn hoặc kéo dài. Những vector đó chính là Eigenvectors.

Dưới đây là trình bày chi tiết về khái niệm và tính chất đặc trưng của từng yếu tố:

Eigenvalues là gì?

Eigenvalues (giá trị riêng) là các giá trị vô hướng đặc trưng được gắn với các Eigenvector của ma trận. Chúng cho biết mức độ co giãn hoặc nén mà một Eigenvectors phải chịu khi trải qua phép biến đổi tuyến tính.

Tính chất của Eigenvalues:

• Nếu eigenvalue dương, vector giữ nguyên hướng nhưng thay đổi độ dài.
• Nếu eigenvalue âm, vector sẽ bị đảo ngược hướng.
• Giá trị tuyệt đối của eigenvalue càng lớn thì mức độ co giãn càng mạnh, đồng nghĩa hướng đó có vai trò quan trọng hơn trong việc biểu diễn dữ liệu.

Eigenvectors là gì?

Eigenvectors (vector riêng) là những vector đặc biệt giữ nguyên hướng khi chịu tác động bởi một ma trận. Những vector này chỉ bị kéo dài, rút ngắn hoặc đảo chiều. Nói cách khác, Eigenvectors biểu diễn các hướng bất biến của phép biến đổi. 

Trong PCA, Eigenvectors xác định các trục chính mà dữ liệu có phương sai lớn nhất. Điều này giúp chúng ta dễ dàng hình dung và phân tích dữ liệu hơn.

Tính chất: Eigenvectors đại diện cho các hướng "ổn định" hoặc "bất biến" của một phép biến đổi.

Cách tính Eigenvalues và Eigenvectors

Để tính Eigenvalues và Eigenvectors, cần làm việc với một ma trận vuông và áp dụng phương trình đặc trưng.

Phương trình đặc trưng

Phương trình đặc trưng là công cụ chính giúp tìm ra các Eigenvalues. Sau khi đã biết Eigenvalues, chúng ta sẽ sử dụng kết quả này để giải một hệ phương trình tuyến tính, từ đó tìm ra Eigenvector tương ứng.

Bước 1: Bắt đầu từ phương trình biến đổi ma trận

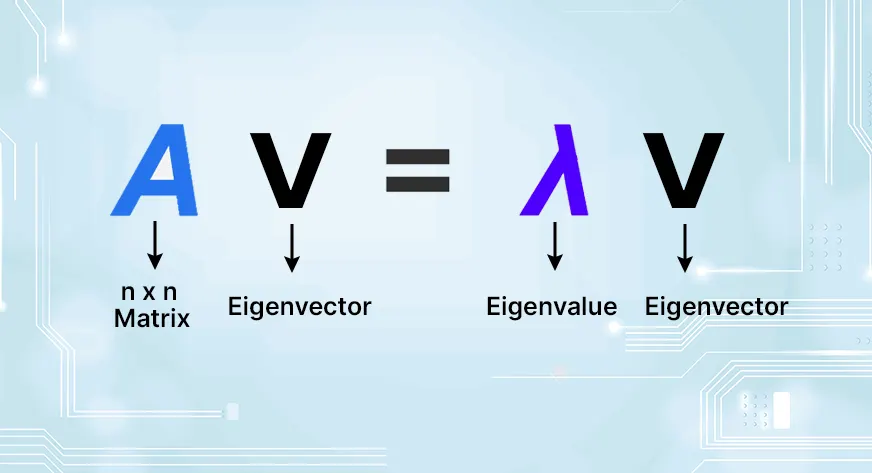
Mối quan hệ giữa ma trận A, Eigenvectors v và eigenvalue λ  được xác định bởi phương trình:

Av=λv

Trong đó:

• A: ma trận vuông (n×n)
• v: vector riêng khác 0 (Eigenvector)
• λ: giá trị vô hướng (Eigenvalue)

Bước 2: Sắp xếp lại phương trình

Để tìm λ, cần sắp xếp lại phương trình, thực hiện chuyển vế phải sang vế trái và đổi dấu, ta có:

Av − λv=0

• Ở bước này, ta có thể đặt v làm nhân tử chung. Tuy nhiên, vì A là ma trận và λ là một số vô hướng, nên không thể thực hiện phép trừ trực tiếp (A − λ). Vì vậy, chúng ta cần nhân λ với một ma trận đơn vị (I) có cùng kích thước với A. 
• Ma trận đơn vị là một ma trận vuông có các số 1 trên đường chéo chính và các số 0 ở các vị trí khác (ví dụ ma trận đơn vị 3×3):

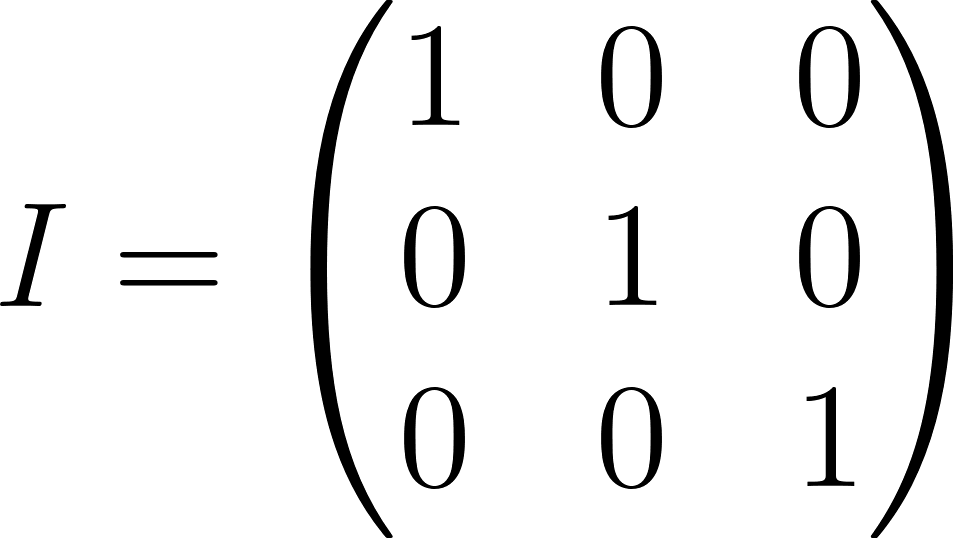
Khi nhân v với I, phương trình của chúng ta sẽ trở thành:

(A − λI)v=0

Bước 3: Thiết lập định thức

Để phương trình (A − λI)v=0 có nghiệm v ≠ 0, ma trận (A−λI) phải có định thức (determinant) bằng 0 (Lý do là vì Eigenvector không thể là vector 0). Kết quả, chúng ta có phương trình đặc trưng như sau:

det(A − λI)=0

Việc giải phương trình này sẽ cho chúng ta kết quả của cả Eigenvalues λ và Eigenvectors v. 

Các bước tính toán

Dưới đây là các bước tính toán cụ thể để tìm ra Eigenvalues λ và Eigenvectors v:

Bước 4: Tìm Eigenvalues (λ)

Giả sử chúng ta có một ma trận A:

Thay A vào phương trình đặc trưng det(A−λI)=0, phương trình trở thành:

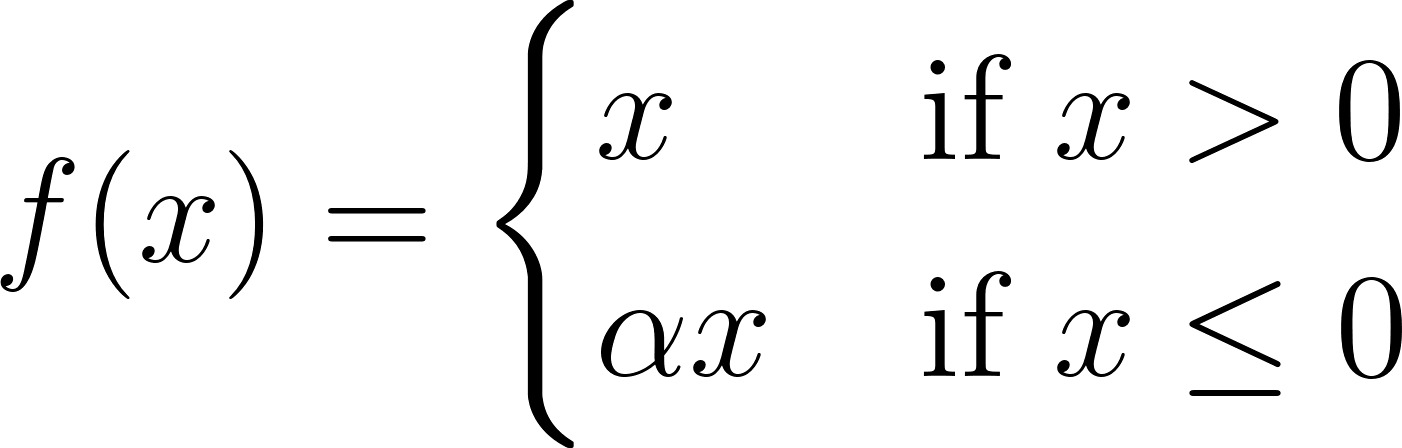
Tính định thức, ta sẽ nhận được phương trình bậc hai:

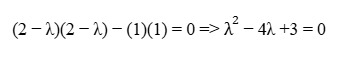
Giải phương trình bậc hai này, ta sẽ tìm được các giá trị của Eigenvalues λ.

Bước 5: Giải Eigenvectors (v)

Sau khi đã tìm được các Eigenvalues λ, chúng ta quay lại phương trình ban đầu:

(A−λI)v=0

Lần lượt thay từng giá trị của λ, A và I vào phương trình này, sau đó giải hệ phương trình tuyến tính, ta thu được vector v tương ứng cho mỗi Eigenvalue.

Các phương pháp tính toán số

Khi ma trận có kích thước lớn, việc giải bằng tay gần như bất khả thi. Lúc này, bạn cần áp dụng các công cụ lập trình hỗ trợ tính toán số. Ví dụ như: :

• Thuật toán QR (QR Algorithm): Đây là một phương pháp phổ biến để tìm Eigenvalues. Thuật toán này sử dụng một chuỗi các phép phân tích ma trận (phân tích QR) để lặp lại và hội tụ về các Eigenvalues.
• Phân tích Cholesky hoặc LU: Đối với một số loại ma trận nhất định (ví dụ: ma trận đối xứng hoặc xác định dương), các phương pháp chuyên biệt như phân tích Cholesky hoặc LU có thể được sử dụng để nâng cao hiệu quả tính toán.
• Cân bằng và tỷ lệ hóa: Để cải thiện sự ổn định số học, các ngôn ngữ lập trình như R và Python thường được áp dụng để điều chỉnh tỷ lệ và cân bằng ma trận trước khi thực hiện các phép tính.

Ứng dụng của Eigenvalues và Eigenvectors

Eigenvalues và Eigenvectors giữ vai trò quan trọng trong nhiều lĩnh vực khoa học, công nghệ và trí tuệ nhân tạo như:

• Thuật toán PageRank của Google: Xác định mức độ quan trọng của từng trang web dựa trên Eigenvectors ứng với eigenvalue 1 của ma trận liên kết.
• Quá trình Markov & phân tích trạng thái ổn định: Dùng trong mô phỏng, xử lý ngôn ngữ tự nhiên, hệ thống gợi ý và các mô hình ngẫu nhiên. Trong mô hình này, Eigenvector tương ứng với Eigenvalue lớn nhất (trong PageRank thường là 1) của ma trận liên kết, thể hiện xác suất ổn định lâu dài của hệ thống.
• Principal Component Analysis (PCA): Sử dụng Eigenvectors để xác định các trục chính có phương sai lớn nhất của dữ liệu, từ đó loại bỏ nhiễu và rút trích các đặc trưng chính. Kỹ thuật này được ứng dụng phổ biến trong các lĩnh vực học máy, nhận diện hình ảnh và nén dữ liệu.
• Xử lý ngôn ngữ tự nhiên (Natural Language Processing − NLP): Ứng dụng trong Phân tích ngữ nghĩa tiềm ẩn (Latent Semantic Analysis - LSA), mô hình hóa chủ đề (topic modeling), word embeddings. Điều này giúp phát hiện quan hệ ngữ nghĩa giữa các từ và cải thiện các tác vụ như tìm kiếm, phân cụm văn bản, xây dựng hệ thống gợi ý,....
• Phân tích phổ đồ thị: Dựa trên Eigenvalues của ma trận Laplacian để phát hiện cộng đồng, phân cụm dữ liệu và đo lường độ kết nối trong mạng xã hội, mạng máy tính,.....
• Thị giác máy tính: Eigenvectors được ứng dụng trong phương pháp Eigenfaces để nhận diện và so sánh khuôn mặt. Bằng cách trích xuất các thành phần chính của khuôn mặt, công nghệ này giúp các hệ thống nhận dạng hoạt động hiệu quả hơn.
• Ổn định hệ thống và robot: Eigenvalues của ma trận hệ thống quyết định sự ổn định, khả năng hội tụ trong điều khiển tự động và thuật toán học máy.
• Xử lý tín hiệu & truyền dữ liệu: Eigen-decomposition (phân tách theo vector riêng) hỗ trợ tối ưu kênh truyền, bằng cách phân tách tín hiệu, trích chọn đặc trưng và lọc nhiễu.

Tạm kết

Hy vọng rằng bài viết này đã mang đến cho bạn cái nhìn rõ ràng hơn về Eigenvalues và Eigenvectors. Không chỉ dừng lại ở những khái niệm toán học thuần túy, chúng chính là “chìa khóa” để mở ra nhiều ứng dụng quan trọng trong thực tiễn: từ tối ưu hóa thuật toán tìm kiếm, giảm chiều dữ liệu trong học máy, đến xử lý tín hiệu và đảm bảo ổn định hệ thống. Việc nắm vững hai khái niệm này sẽ giúp các doanh nghiệp, tổ chức và cả cá nhân xây dựng nền tảng vững chắc để khai thác hiệu quả các công nghệ lõi của kỷ nguyên số.